Exploring an ODE with Euler method
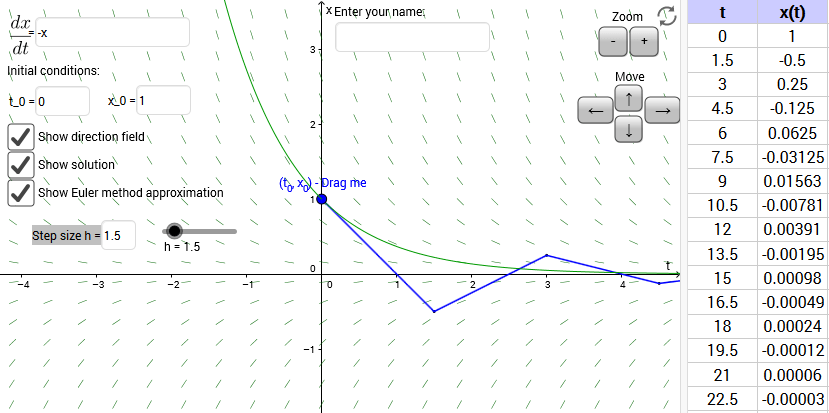
This applet displays the direction field and solutions for an ordinary differential equation (ODE), and calculates approximate solutions using Euler’s method.
Enter the ODE in the textbox for $\frac{dx}{dt}$. Set the initial condition $(t_0, x_0)$ by dragging the point or entering values in the textboxes.
Click ‘Show solution’ to display the solution of the ODE subject to the given initial condition.
Click ‘Show direction field’ to display the direction field for the ODE. What is the relationship between the direction field and the solution curve?
Click ‘Show Euler method approximation’ to approximate the solution using Euler’s method. Set the step size $h$ using the slider or textbox. The curve produced by Euler’s method is shown in blue, and the calculated values are shown in the spreadsheet on the right. How does the approximation (blue) compare to the exact solution (green)?
Other resources: