Convergence and continuity of a function
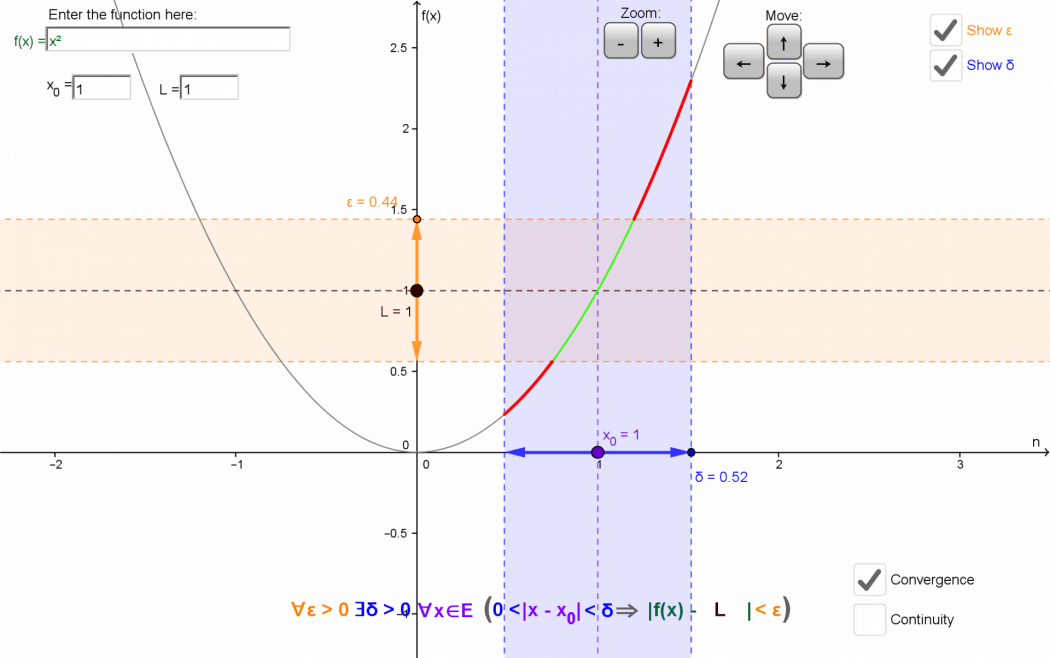
This applet illustrates the ε-δ definitions of the limit and continuity of a function.
Enter a rule for the function $f(x)$ in the box provided.
Drag the purple point on the x-axis to adjust $x_0$, and the brown point on the y-axis to adjust L.
Click Show ε or Show δ to display regions for ε and δ. Drag the edges of the orange or blueregions to adjust ε or δ. For each ε, can you find a δ so that all of the curve in the blue region is also in the orange region?
Zoom in or out using the buttons, if needed.
Use the checkboxes at bottom-left to switch between convergence $\Bigl( \displaystyle \lim_{x \to x_0} f(x) = L \Bigr)$ and continuity $\Bigl( \displaystyle \lim_{x \to x_0} f(x) = f(x_0) \Bigr)$.
Some interesting functions to try:
-
A function with a single point discontinuity:
f(x) = If[ 0.99 < x < 1.01, 2, x ]
Does the limit exist at x = 1? Is it continuous at x = 1? -
The Dirichlet function $\begin{cases} 1 & \text{ if } x \in \mathbb{Q} \\ 0 & \text{ if } x \notin \mathbb{Q}\end{cases}$. Enter this function as
f(x) = d(x)
Where, if anywhere, does the limit exist? -
A variation on the Dirichlet function: $\begin{cases} x^2 + 1 & \text{ if } x \in \mathbb{Q} \\ 1 & \text{ if } x \notin \mathbb{Q}\end{cases}$.
Enter this as
f(x) = d(x)*x^2 + 1
Where does the limit of this function exist? Where is it continuous?
Other resources: