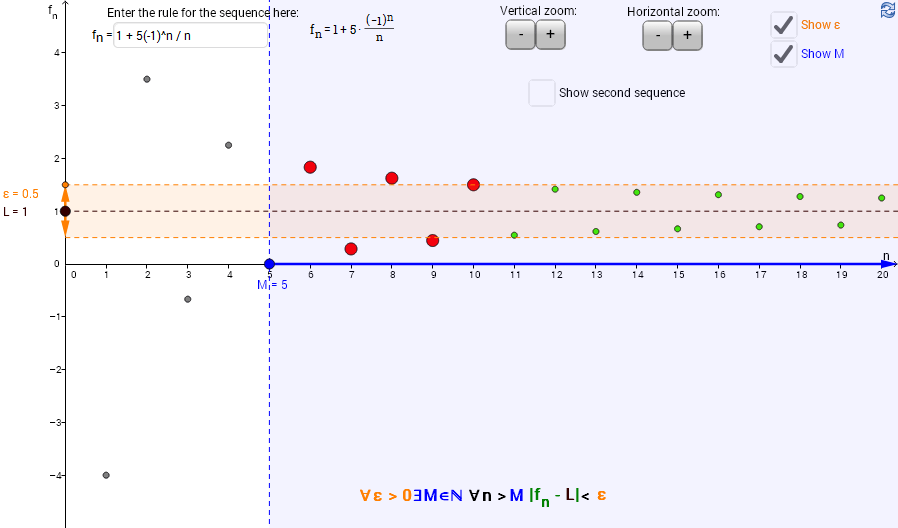
Convergence of a sequence
This applet illustrates the ε-M definition of convergence of a sequence.
Enter a rule for the sequence $f_n$ in the box provided.
Drag the green point to adjust the value of L.
Click Show ε or Show M to display points for ε and M, and their corresponding regions. For each ε, can you find an M so that all points in the blue region are also in the orange region?
Zoom in or out using the buttons, if needed.
You can add a second sequence for comparison by enabling 'Show second sequence'.
Some interesting sequences to try:
- $f_n = (-1)^n$ – enter this as $f_n$ =
(-1)^n - $f_n = (-1)^n/n$ – enter this as $f_n$ =
(-1)^n/n - $f_n = \sin(n)$
- $f_n = (1+1/n)^n$
– enter this as $f_n$ =
(1+1/n)^n
Other resources: