Differentiability of a function

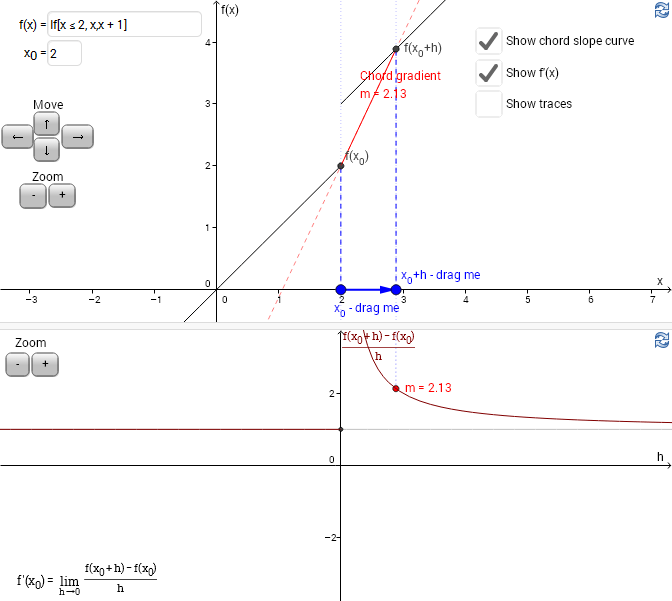
This applet illustrates the definition of derivative as the limit of the gradient of a chord.

The upper section shows the graph of $f(x)$, and a chord from a point $(x_0,f(x_0))$ to $(x_0+h,f(x_0+h))$.

Drag the points $x_0$ and $x_0+h$ to change them. What do you get as $h \to 0$?

Recall that the derivative of $f$ at the point $x_0$ is defined as \[ f'(x_0) = \lim_{h \to 0} \frac{f(x_0+h) – f(x_0)}{h} \]

that is, as a limit of the chord gradient function $m(h)$.

Click 'Show chord slope curve' to show in the lower pane a plot of the chord gradient function $m(h)$, as a function of $h$.

Click 'Show derivative' to add a plot of $f'(x)$. What happens to $f'(x)$ and $m(h)$ at $h = 0$?

Some interesting functions to try:

The absolute value function |x|: enter this as f(x) = abs(x)
Is this function differentiable at x = 0? At x ≠ 0?
A function with a single point discontinuity: f(x) = If[ 0.98 < x < 1.02, 2, x ]
Is the function differentiable at x = 1?
A function with a step discontinuity: f(x) = If[x < 1, x, x+1]
Is the function differentiable at x = 1?
The Dirichlet function $d(x) = \begin{cases}1 & \text{ if } x \in \mathbb{Q} \\ 0 & \text{ if } x \notin \mathbb{Q}\end{cases}$. Enter this as f(x) = d(x)
Is this function differentiable?
A variation on the Dirichlet function: $d(x) = \begin{cases}x^2 + 1 & \text{ if } x \in \mathbb{Q} \\ 1 & \text{ if } x \notin \mathbb{Q}\end{cases}$. Enter this as f(x) = d(x)*x^2 + 1
Where is this function differentiable?

Other resources: