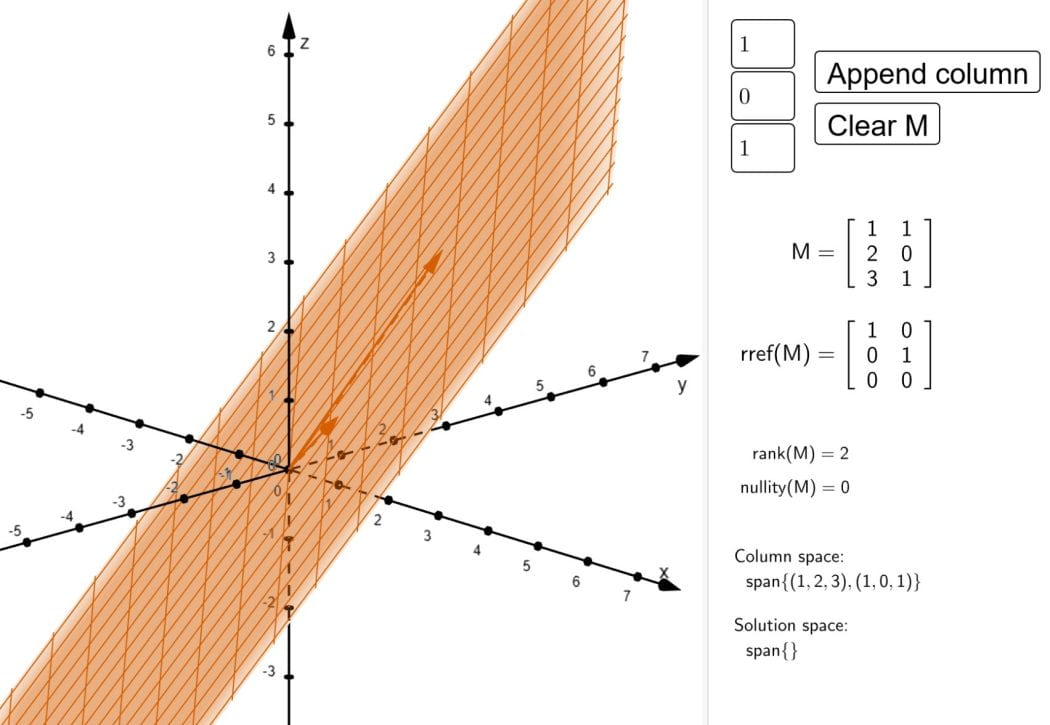
Columns of a matrix and the rank-nullity theorem
This applet shows how the column space, solution space, rank and nullity of a matrix M change as you append additional columns.
Initially the matrix M has a single column. You can add extra columns to M by editing the text boxes on the right of the applet, and clicking the ‘Append column’ button.
The rank-nullity theorem states that the rank of M plus the nullity of M is equal to the number of columns of M. Notice that every time you append a column to M, either the rank goes up by 1, or the nullity of M goes up by 1, depending on whether that column has a leading entry or not. Can you see why this is consistent with the rank-nullity theorem?
Other resources: