Tag: Linear algebra
-
Bases and Coordinates in R2
This applet demonstrates the concept of co-ordinate vectors in R^2.melbapplets.ms.unimelb.edu.au/2024/04/05/bases-and-coordinates-in-r2
-
Visualising the Gram-Schmidt Algorithm
This applet demonstrates the Gram-Schmidt algorithm performed in R^3.melbapplets.ms.unimelb.edu.au/2024/04/05/visualising-the-gram-schmidt-algorithm
-
Visualising linear transformations in R2
This applet shows the geometric effect of a linear transformation T: R^2 → R^2.melbapplets.ms.unimelb.edu.au/2024/03/25/visualising-linear-transformations-in-r2
-
Visualising linear transformations in R3
This applet shows the geometric effect of a linear transformation T in R^3.melbapplets.ms.unimelb.edu.au/2024/03/25/visualising-linear-transformations-in-r3
-
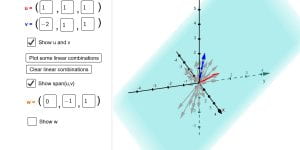
Visualising the span of two vectors
This applet visualises the span of two vectors in R3 using linear combinations.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-the-span-of-two-vectors
-
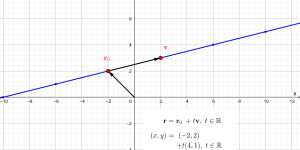
Vector equations of lines in R2
This applet shows a line in R2 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-lines-in-r2
-
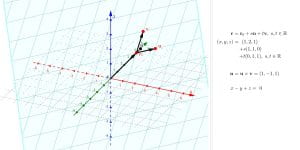
Vector equations of planes in R3
This applet shows a plane in R3 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-planes-in-r3
-
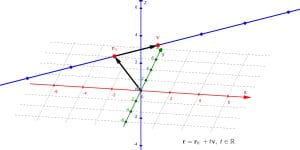
Vector equations of lines in R3
This applet shows a line in R3 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-lines-in-r3
-
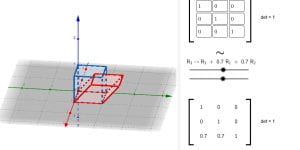
Visualising row addition on a 3×3 matrix
This applet shows how the determinant is unaffected by the elementary row operation of addition of a scalar multiple of a row to another row.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-row-addition-on-a-3x3-matrix
-
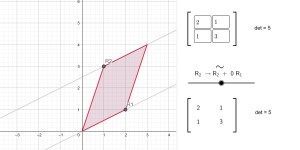
Visualising row addition on a 2×2 matrix
This applet shows how the determinant is unaffected by the elementary row operation of addition of a scalar multiple of a row to another row.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-row-addition-on-a-2x2-matrix
Number of posts found: 14