Tag: MAST10007
-
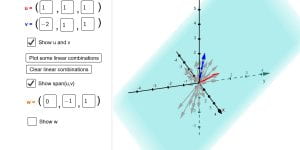
Visualising the span of two vectors
This applet visualises the span of two vectors in R3 using linear combinations.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-the-span-of-two-vectors
-
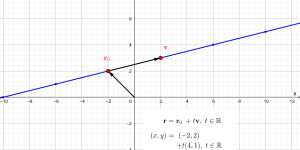
Vector equations of lines in R2
This applet shows a line in R2 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-lines-in-r2
-
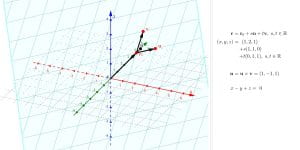
Vector equations of planes in R3
This applet shows a plane in R3 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-planes-in-r3
-
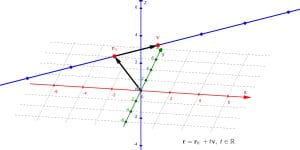
Vector equations of lines in R3
This applet shows a line in R3 and the vector form of its equation.melbapplets.ms.unimelb.edu.au/2023/02/01/vector-equations-of-lines-in-r3
-
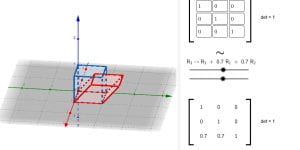
Visualising row addition on a 3×3 matrix
This applet shows how the determinant is unaffected by the elementary row operation of addition of a scalar multiple of a row to another row.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-row-addition-on-a-3x3-matrix
-
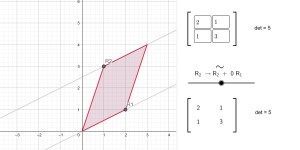
Visualising row addition on a 2×2 matrix
This applet shows how the determinant is unaffected by the elementary row operation of addition of a scalar multiple of a row to another row.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-row-addition-on-a-2x2-matrix
-
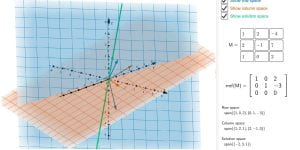
Visualising row, column and solution spaces
This applet shows the row, column, and solution spaces of a 3x3 matrix M.melbapplets.ms.unimelb.edu.au/2023/02/01/visualising-row-column-and-solution-spaces
-
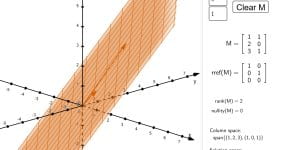
Columns of a matrix and the rank-nullity theorem
This applet shows how the column space, solution space, rank and nullity of a matrix M change as you append additional columns. Initially the matrix M has a single column. You can add extra columns to M by editing the text boxes on the right of the applet, and clicking the ‘Append column’ button. The […]melbapplets.ms.unimelb.edu.au/2023/02/01/columns-of-a-matrix-and-the-rank-nullity-theorem
-
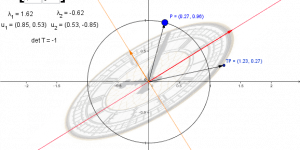
Linear transformations and eigenvectors
This applet illustrates the effect of a linear transformation in R2 on the unit circle/unit disk, and the geometric meaning of eigenvectors, eigenvalues and determinant.melbapplets.ms.unimelb.edu.au/2021/07/12/linear-transformations-and-eigenvectors
-
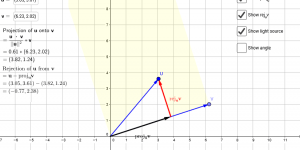
Vector projections
This applet aims to demonstrate visually the projection of a vector u onto a vector v.