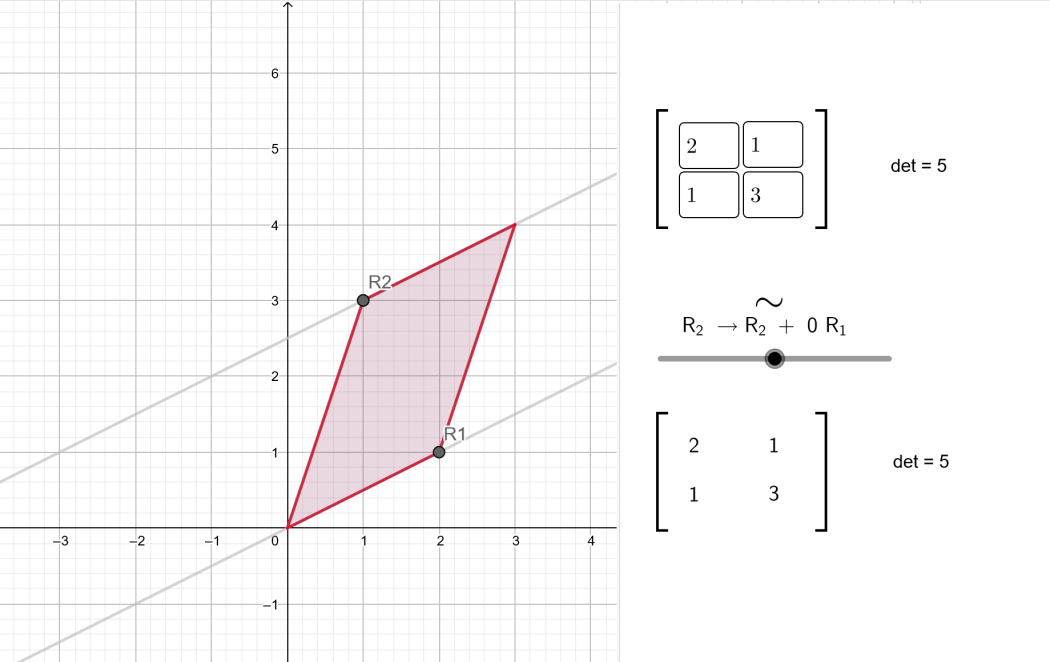
Visualising row addition on a 2×2 matrix
This applet shows how the determinant is unaffected by the elementary row operation of addition of a scalar multiple of a row to another row.
The determinant of a 2×2 matrix A is equal to the signed area of the parallelogram whose edges are given by the rows of A.
The parallelogram in blue has edges given by the rows of the first matrix, and the parallelogram in red has edges given by the rows of the second matrix, obtained by adding a multiple of row 1 to row 2. Use the slider to change the multiple.
Both parallelograms share a base, and the height perpendicular to the base is always the same, regardless of the value of the scalar. This shows that the two parallelograms have the same area.
Other resources: