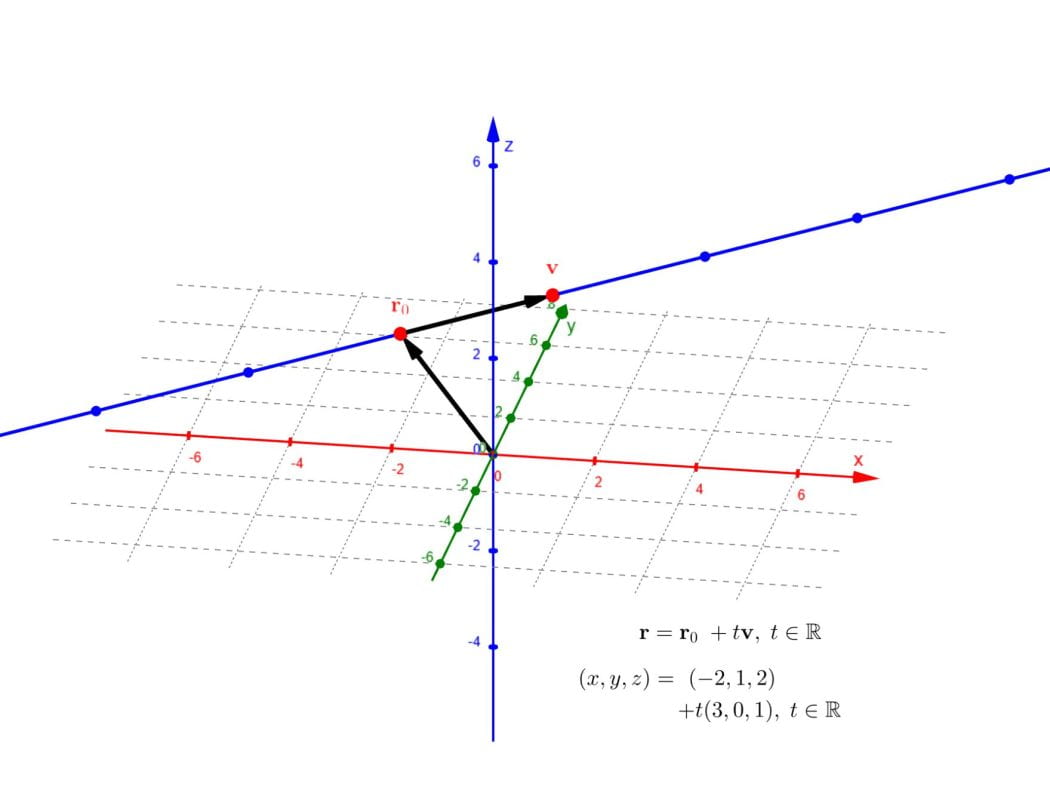
Vector equations of lines in R3
This applet shows a line in ℝ3 and the vector form of its equation.
A vector equation for a line has the form r = r0 + tv, t ∈ ℝ where r0 is the position vector of a point on the line, and v is a vector parallel to the line.
You can click and drag r0 and v to adjust the line.
Try modifying both r0 and v in turn, to see what the resulting lines have in common.
By default you can only move the points horizontally (parallel to the xy-plane); if you wish to switch between moving the points horizontally or vertically, click on the point a second time.
If you select the “Constrain points to line” checkbox, the line will be locked in place, and r0 and v will only be able to be moved along the line. This allows you to see that the same line can have many possible vector equations.
Other resources:
Related applet: Vector equations of planes in R3