Tag: MAST10021
-
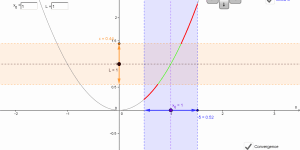
Convergence and continuity of a function
This applet illustrates the ε-δ definitions of the limit and continuity of a function. It can be used to investigate (non-)convergence or (dis)continuity of real functions, including the Dirichlet everywhere discontinuous function and variants.melbapplets.ms.unimelb.edu.au/2021/07/12/convergence-and-continuity-of-a-function
-
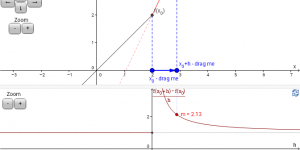
Differentiability of a function
This applet illustrates the definition of derivative as the limit of the gradient of a chord.melbapplets.ms.unimelb.edu.au/2021/07/12/differentiability-of-a-function
-
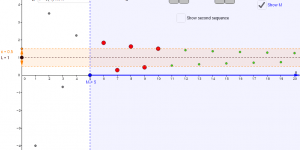
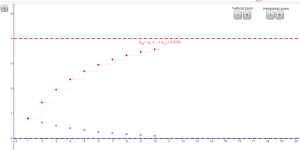
Convergence of a sequence
This applet illustrates the ε-M definition of convergence of a sequence.melbapplets.ms.unimelb.edu.au/2021/07/12/convergence-of-a-sequence
-
Sequences and series
This applet shows the relationship between terms of a sequence and the partial sums of a series. It also allows exploration of some important sequences & series including geometric and harmonic sequences.melbapplets.ms.unimelb.edu.au/2021/07/09/sequences-and-series
-
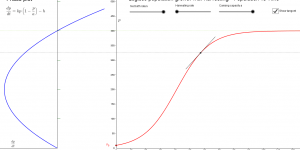
Logistic population growth
This applet explores a logistic population growth model with no harvesting. The phase plot is shown alongside the plot of p vs t.melbapplets.ms.unimelb.edu.au/2021/07/09/logistic-population-growth
-
Logistic population growth with harvesting
This applet explores a logistic population growth model with constant harvesting.melbapplets.ms.unimelb.edu.au/2021/07/09/logistic-population-growth-with-harvesting
-
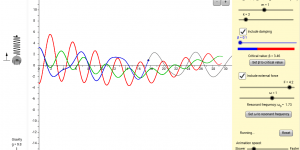
Model of a spring with drag and forcing
This applet simulates a spring acting under gravity, subject to drag and an external driving force.melbapplets.ms.unimelb.edu.au/2021/07/09/model-of-a-spring-with-drag-and-forcing
-
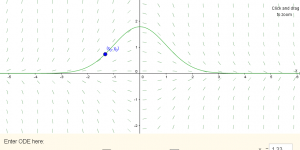
Exploring an ODE
This applet displays the direction field and solutions for an ordinary differential equation (ODE).